Matt in a Tux

[I’ve been looking at this for awhile, and it may not even be an interesting topic anymore, but I decided I would have a quick attempt at working through it. This was mostly done in a wrote this on a cocktail napkin fashion, as well. Comments and criticisms would be great, too!]

I’d like to suggest that time is not infinite, and, in fact, “infinity” should not be used practically, but only theoretically.

Let a=1/3 and b=.33… (where ‘…’ indicates repeating to infinity).
1/3=.33…
a=b
3(1/3)=1
3(.33…)=.99…
3(a)=1
3(b)=.99…
a does not equal b, after a simple multiplication. (I understand this can be shown with limits as well.) But a=b seems obviously and necessarily true.

So, .99… = 1 seems like it must be true somehow.

With a set containing an infinite set of numbers, it is represented by the infinity symbol.
With a set containing an infinite set of time places, I will represent it with S^t0-tn.

How is it ok to represent infinite time like this?
“Infinity” is an abstract conception. So, this can be an abstract confession as well; we can see how it is possible to represent and split infinity into parts.

First, in common usage, one typically has no problem mentioning “half an hour” or “36.48 seconds”. Time has been indexed at a certain point in one case, and has been split in the other case.

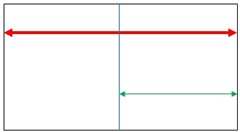
The following diagram will be used in the proceeding paragraph as tool to demonstrate another supporting reason.

The red line represents an infinite area of measurement. The blue line represents a line splitting the infinite area of measurement. And the green line represents the new infinite are of measurement. Eventually, since the infinite area can be split, an infinite area will eventually decrease to a .00…1 where it would eventually become 0 (by the same principle as demonstrated earlier).

So, we can now say this:
(S^t1/3^ S^t1/3^ S^t1/3)=S^t0-tn
(S^t.33…^ S^t.33…^ S^t.33...)=S^t0-tn

The latter suggests infinite time while the former suggest a finite time.

How do we decide?
To have infinite time, we’d have to accept that a does not equal b, i.e. 1/3 does not equal .33…). However, a=b seems obvious and necessary.

Infinity is simply a notion that should be used only in theorizing, and rarely, if at all, in practical application.

(I’d also like to note that this fits perfectly with a deterministic view of things, which can be for a different time.)